Er KBU lodtrækningen tilfældig?

Den halvårlige lodtrækning om turnus-pladserne er netop overstået. Som altid er der nok at sludre om – hvem har fået gode og dårlige numre? Kan man få et ”godt” turnus forløb? Og er lodtrækningen nu også foregået tilfældigt?

Det sidste spørgsmål er jo lidt sjovt. Så lad os prøve at finde ud af det.

På basislaege.dk kan man se hvilke byer har fået tildelt hvilke numre. Der er 177 nye læger fra KU, 129 fra AU og 64 fra SDU, 370 i alt. Jeg har hentet data ned og fjernet de 4 der har fået tildelt særlige hensyn.

Lige mange lave og høje numre i byerne?

Hvis vi deler de 370 numre op i 10 grupper, således at nummer 1 til 37 er gruppe 1, nummer 38 til 74 er gruppe 2, osv., burde KU, AU og SDU have hhv. omkring 48 %, 35 % og 17 % i hver gruppe. Det svare til ca. 18, 13 og 6 numre i hver af de 10 grupper. Altså hvis der ikke er nogle byer der er blevet forfordelt.

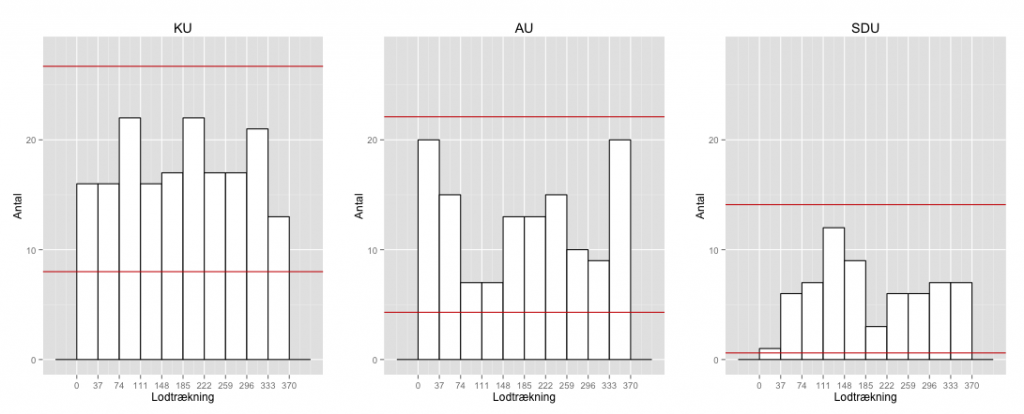
Det første vi kan gøre er derfor bare at kigge på om hver by fordeler sig uniformt i de 10 grupper:

For KU passer antagelsen jo temmelig godt – der er næsten ingen forskel på de enkelte grupper. For AU og SDU ser mindre fordelingen mindre uniforme ud. En let måde at understrege dette på er at kigge på median og gennemsnit – hvis data fordeler sig uniformt vil de to tal nemlig være meget ens:

Gennemsnit / Median
KU: 184.64 / 186
AU: 184.05 / 193
SDU: 190.84 / 168

Så for AU og SDU er tallene altså en smule skæve. Men i gennemsnit er AU’erne ikke blevet forfordelt. Vi stakkels SDU studerende har desværre fået lidt højre numre i snit, men en simpel ANOVA fortæller os der ikke er nogen forskel på AU’s, KU’s og SDU’s tal.

Men der er nu alligevel mange AU’er der falder i de gode gruppe 1 og 2. Kan det virkelig være tilfældigt opstået?

Simulation

En måde at svare det på kunne være at simulerer 1000 nye lodtrækninger, hvilket jeg har gjort med følgende R kode:

[code language=”r”]
library(permute)

hbreaks = seq(0,370,by=37) #variabel for breaks

df_sdu_rand <- data.frame() #generate empty df’s to fill up
df_au_rand <- data.frame()
df_ku_rand <- data.frame()

for(i in 1:1000) { #loop
rand_n370 <- shuffle(370)
sdu_rand <- rand_n370[1:64]
au_rand <- rand_n370[65:193]
ku_rand <- rand_n370[194:370]

h_sdu <- hist(sdu_rand, breaks = hbreaks, plot = FALSE)
h_au <- hist(au_rand, breaks = hbreaks, plot = FALSE)
h_ku <- hist(ku_rand, breaks = hbreaks, plot = FALSE)

#Grupper af 10
df_sdu_rand <- rbind(df_sdu_rand, h_sdu$counts)
df_au_rand <- rbind(df_au_rand, h_au$counts)
df_ku_rand <- rbind(df_ku_rand, h_ku$counts)
}
[/code]

Ud af de 1000 nye lodtrækninger er der ingen der kommer over eller under de røde linjer på figur 1. Hvis der var tal i den rigtige lodtrækning der lå herunder eller over, ville det altså være mistænksomt.

SDU kommer tæt på, da kun 1 person i datasættet har fået tildelt under 37 – men det kan altså være tilfældigt, omend det kun sker i 5 gange i mine 1000 simulationer (altså i 0,5 % af tilfældene), at SDU kun får 1 i gruppe 1.

Men datasættet snyder. Der mangler nemlig nogle tal, idet personer der har trukket nummer, men ikke vil vælge forløb ikke er på. Nu ved jeg tilfældigvis at et af de numre der ikke er på listen, nemlig nummer 11, er tildelt en SDU’er, hvorfor SDU altså har 2 i denne gruppe (det sker i ca. 3 % af min simulationer at SDU kun får 2 i gruppe 1).

Stadig ingen rygende pistol. Vi må hive det tunge skyts frem.

Er det sidste ciffer tilfældigt?

Inden for den politiske verden er man også meget interesseret i om der bliver snydt, fx ved et valg. En metode er Benford’s Law, men den kan ikke vi bruge her da vi kun har tal op til 370.

En anden er Beber og Scacco’s last digit (”sidst ciffer”) metode. Her kigger man på sidste ciffer blandt en række tal. Alle tal mellem 0 og 9 burde optræde lige hyppigt som det sidste ciffer. Da mennesker ofte er dårlige til at finde på tilfældige tal, genbruger de ofte de samme cifre, så hvis tallene ikke er uniformt fordelt, kunne det tyde på snyd.

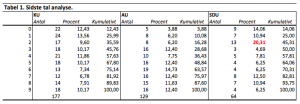
Lad os se hvordan tallene ser ud for de enkelte byer:

Hvad er nu det for noget? Her stikker SDU’s tre-taller jo ud. Lidt over 20% af de sidste cifre er tallet 3, hvilket umiddelbart er lidt underligt. Det burde jo være omkring 10 %. Svaret skal nok findes i at der kun trækkes 64 numre til Odense, hvorfor risikoen for en skæv fordeling er høj.

Lad os igen prøve at simulerer 1000 tilfældige lodtrækninger, hvilket er gjort med følgende kode (med hjælp fra Peter Flom):

[code language=”r”]
n <- 1000
maxes <- vector("numeric", n)
for (i in 1:n)
{
x <- sample(0:9, 64, replace=TRUE)
maxes[i] <- max(table(x)/64)
}
sum(maxes > 0.20)/n
[/code]

Ideen er at generer 64 tilfældige tal mellem 0 og 9 og hver gang udvælger det tal der optræder hyppigst, og så regne ud hvor stor en procentdel det udgør. Det gør vi så 1000 gange. Dernæst kan vi så spørge: hvor ofte sker det blandt 64 tilfældige tal, at et ciffer optræder mere end 20 % af tilfældene?

Svaret er lidt overraskende, at det sker i ca. 17 % 10 % af tilfældene! ”Sidst-ciffer” testen er altså ikke speciel god når vi vil checke SDU’s 64 numre.

Hvis vi derimod køre samme test på 177 (det antal numre der blev trukket på KU) i stedet for 64, er der kun 0.1% 0 % chance for at et ciffer optræder mere end 20% af tiden.

Konklusion

De numre de enkelte byer er blevet tildelt kan godt være opstået tilfældigt, og det virker derfor ikke til at onde bureaukrater har forfordelt nogle byer.